ปฏิบัติการ "ราหูอมจันทร์".....วัดระยะทางจากโลกถึงดวงจันทร์ "Operation Rahu Episode I"

          วันที่ 15 เมษายน 2557 เกิดปรากฏการณ์ "จันทรุปราคาเต็มดวง" ที่ทวีปอเมริกาเหนือ เผอิญผมอยู่ที่บ้าน Broken Arrow รัฐ Oklahma USA จึงได้โอกาสสังเกตการณ์ ถ่ายภาพและเก็บข้อมูลสำหรับคำนวณระยะทางจากโลกไปยังดวงจันทร์ โดยใช้ภูมิปัญญาวิชาดาราศาสตร์และคณิตศาสตร์ของกรีกโบราณสองพันกว่าปีที่แล้ว

 

 

คืนวันที่ 14 ต่อเนื่องถึง 15 เมษายน 2557 ผมอยู่ที่บ้าน Broken Arrow รัฐ Oklahoma สหรัฐอเมริกา ทราบมาก่อนแล้วว่าคืนนี้จะเกิดปรากฏการณ์ "จันทรุปราคาเต็มดวง" ราวๆหลังเที่ยงคืน 

 

 

      จันทรุปราคาเกิดขึ้นได้อย่างไร

          ปรากฏการณ์ทางดาราศาสตร์ที่เรียกว่า "จันทรุปราคา" หรือ "จันทรคาส" มาจากรากศัพท์ภาษาสันสกฤต "Chandra Grahan" chandra = ดวงจันทร์ Grahan = คราส หรือ เงา ถ้าดวงอาทิตย์ โลก และดวงจันทร์ โคจรมาอยู่ในแนวเส้นตรงเดียวกัน เงาของโลกจะบดบังดวงจันทร์จนมืดมิดชั่วระยะเวลาหนึ่ง คนอินเดียและคนไทยเรียกปรากฏการณ์นี้ว่า "ราหูอมจันทร์" (ท่านที่สนใจที่มาของเรื่องราหูอมจันทร์ โปรดอ่านในคอลั่มอินเดียน่าโจนส์)

 

 

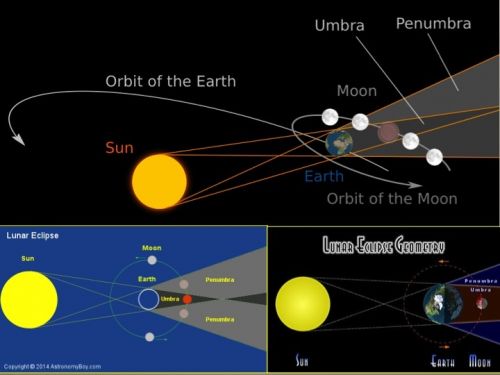
ปรากฏการณ์จันทรุปราคาจะต้องเกิดในวันพระจันทร์เต็มดวง ตามปกติดวงจันทร์จะโคจรเข้าไปอยู่ด้านหลังของโลกแต่อยู่คนละระนาบทำให้มุมมองจากโลกเห็นด้านสว่างที่สะท้อนแสงอาทิตย์แบบเต็มดวง แต่ถ้าดวงจันทร์เข้าไปอยู่ด้านหลังของโลกและเผอิญอยู่ในระนาบเดียวกันทำให้ถูกเงาของโลกบดบัง จึงเกิด "จันทรุปราคา" ซึ่งมีทั้งเต็มดวง และบางส่วน

 

  

 เงาของโลกมีสองลักษณะคือ เงามืด (Umbra) และเงามัว (Penumbra) การเกิดจันทรุปราคาเต็มดวง หรือจันทรุปราคาบางส่วน ดวงจันทร์ต้องเข้าไปอยู่ในโซนของเงามืด

 

 

เงามืดของโลก (หรือของวัตถุใดๆก็ตาม) จะมีความยาวเท่ากับ 108 เท่า ของเส้นผ่าศูนย์กลาง ในที่นี้ผมใช้ข้อมูล "เส้นผ่าศูนย์กลางของโลก" จาก "ปฏิบัติการอีราโต้สทีเนส" เมื่อวันที่ 21 มีนาคม 2555 ระหว่างปราสาทภูเพ็ก กับปราสาทบายน (อ่านรายละเอียดในเว้ปไซด์) เพื่อคำนวณหาเส้นผ่าศูนย์กลางของโลก และคำนวณหาความยาวของเงามืด (Umbra) ได้เท่ากับ 1,321,272 กม.

 

  

 ปฏิบัติการ "อีราโต้สทีเนส" เมื่อวันที่ 21 มีนาคม 2555 ระหว่างปราสาทภูเพ็ก สกลนคร ประเทศไทย กับปราสาทบายน เมืองเสียมราช ประเทศกัมพูชา ได้เส้นรอบวงโลกเท่ากับ 38,451 กม. (อ่านรายละเอียดในคอลั่มปราสาทภูเพ็ก)

 

 

บรรยากาศตอนเย็นวันที่ 14 เมษายน 2557 ดวงจันทร์ขึ้นเต็มดวงสวยงามเหนือท้องฟ้าเมือง Broken Arrow (Tulsa) Oklahoma USA

 

ระหว่างรอเวลาให้ราหูเข้ามาอมจันทร์ ถือโอกาสถ่ายรูปดาวอังคารที่โคจรเข้ามาใกล้โลกเป็นการอุ่นเครื่อง

 

แสดงวงโคจรของดาวอังคารที่เข้ามาใกล้โลก

 

ปรากฏการณ์ "ราหูอมจันทร์" ครั้งนี้เกิดขึ้นในราศีหญิงสาว (Zodiac Virgo) โดยมีดาวฤกษ์ประจำราศีชื่อ Spica อยู่ใกล้ดวงจันทร์

 

เวลาท้องถิ่นของรัฐ Oklahoma USA 12:58 น. วันที่ 15 เมษายน 2557 ราหูเริ่มแผลงฤทธิ์

 

ตีหนึ่งกว่าๆกินเข้าไปประมาณครึ่งดวง

 

ประมาณตีสองดวงจันทร์เกือบมืดหมด ที่เห็นเป็นสีแดงช้ำๆ (copper color) เพราะมีแสงสะท้อนจากโลกไปที่ดวงจันทร์ ประกอบกับแสงที่มองเห็นต้องผ่านชั้นบรรยากาศของโลก มีฝุ่นละอองและความชื้น ทำให้มองเห็นเป็นสีดังกล่าว ภาษาดาราศาสตร์เรียกว่า "พระจันทร์สีเลือด" (Blood Moon) 

 

02:06 มืดเต็มดวง (Total lunar eclipse)

 

 

ดวงจันทร์เริ่มโผล่ออกมาจากเงามืด เวลา 03:24 น.

 

ออกมาได้เกือบครึ่งดวง

 

แสดงเฟสขั้นตอนของราหูอมจันทร์ (ตามเวลามาตรฐานสากล Universal Time: UT) 

 

       นักดาราศาสตร์ชาวกรีกเมื่อสองพันกว่าปีที่แล้ว......ใช้ปรากฏการณ์ "ราหูอมจันทร์เต็มดวง" คำนวณระยะทางจากโลกไปดวงจันทร์

          เริ่มต้นที่นักดาราศาสตร์ชื่อ "อีราโต้สทีเนส" (Eratosthenes) ท่านใช้มุมดวงอาทิตย์ที่เมืองอเล็กซานเดรีย กับเมืองซาอีน คำนวณเส้นรอบวงของโลกได้อย่างไม่ยากนัก (อ่านรายละเอียดในคอลั่มปราสาทภูเพ็ก และเปิดโลกวิทยาศาสตร์) เมื่อได้ระยะทางเส้นรอบวงก็พลิกสูตรคณิตศาสตร์คำนวณหาเส้นผ่าศูนย์กลางโลกได้อย่างง่ายดายโดยใช้สูตรปีธากอรัส 2PiR = เส้นรอบวง 

 

ผลการคำนวณเส้นรอบวงโลกของท่าน "อีราโต้สทีเนส"  (276 - 194 BC) เป็นต้นแบบนำไปสู่การคำนวณระยะทางระหว่างโลกกับดวงจันทร์

 

          นักดาราศาสตร์ชาวกรีกอีกท่านหนึ่ง "อรีสตาชุส แห่งเมืองซาโมส" (Aristarchus of Samos 310 - 230 BC) ใช้ข้อมูลเส้นผ่าศูนย์กลางของโลกไปเข้าสูตรคำนวณระยะทางจากโลกไปถึงดวงจันทร์ โดยใช้การจับเวลาเคลื่อนตัวของดวงจันทร์ผ่านเงาดำมืดของโลกในปรากฏการณ์ "จันทรุปราคาเต็มดวง" ท่านอรีสตาชุสสามารถบอกได้ว่าดวงจันทร์ห่างจากโลก 240,000 ไมล์ หรือ 384,000 กิโลเมตร ซึ่งใกล้เคียงกับข้อมูลขององค์การนาซ่าแห่งสหรัฐอเมริกา 385,000 กิโลเมตร คลาดเคลื่อนไปเพียง 0.26 % เท่านั้น

 

 

         

          ลองมาดูว่าท่าน "อรีสตาชุส" คำนวณระยะทางระหว่างดวงจันทร์กับโลกโดยใช้ปรากฏการณ์ "จันทรุปราคาเต็มดวง" ได้อย่างไร

          1. ท่านรู้ว่าเงามืดของโลก (Umbra) ในอวกาศเป็นรูปสามเหลี่ยมมุมแหลม ยาวเท่ากับ 108 เท่า ของเส้นผ่าศูนย์กลางโลก เมื่อนำข้อมูลขนาดเส้นผ่าศูนย์กลางโลกจากท่านอีราโต้สทีเนส 8,000 ไมล์ มาคูณกับ 108 = 864,000 ไมล์ แสดงว่าเมื่อเกิดปรากฏการณ์จันทรุปราดวงจันทร์จะต้องอยู่ที่ใดที่หนึ่งในระยะทางของเงามืดนี้  

 

เงามืด (Umbra) ของโลก และดวงจันทร์ เป็นรูปสามเหลี่ยมมุมแหลมมีความยาว 108 เท่าของขนาดเส้นผ่าศูนย์กลาง 

           

          2. ปรากฏการณ์ "สุริยุปราคาเต็มดวง" ทำให้รู้ว่าเงามืดของดวงจันทร์ก็ยาวมาถึงพื้นโลกเช่นกัน และเงามืดนี้ก็มีรูปร่างเป็นสามเหลี่ยมมุมแหลมเหมือนกับเงามืดของโลก สามารถเรียกได้ว่าเป็น "สามเหลี่ยมคล้าย" เพียงแต่ต่างกันที่ขนาดเท่านั้น และการที่ดวงจันทร์สามารถบดบังดวงอาทิตย์จนมืดมิดได้ทั้งดวง (Total solar eclipse) เนื่องมาจากขณะนั้นตำแหน่งของดวงจันทร์เป็น "ภาพเสมือน" ขนาดเท่ากับดวงอาทิตย์ เปรียบประหนึ่งเส้นผมบังภูเขาได้  

 

 

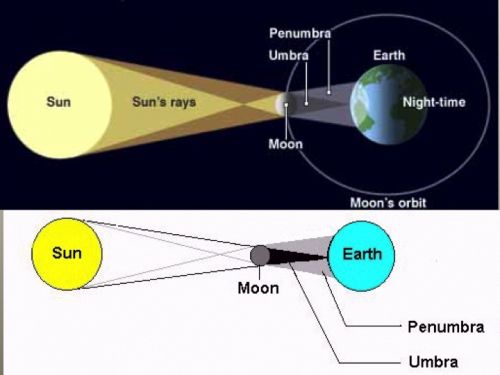
เงามืด (Umbra) ของดวงจันทร์ก็มีลักษณะเดียวกันกับเงามืดของโลก 

 

          3. ท่าน "อรีสตาชุส" จึงสามารถสร้างภาพ "เรขาคณิต" ของปรากฏการณ์จันทรุปราคาเต็มดวง โดยใช้หลักการของ "สัดส่วน สามเหลี่ยมรูปคล้าย" โดยตั้งสมมุติฐานว่าเงามืดของดวงจันทร์ยาวลงมาถึงโลกดังภาพ 

 

 

 

           

           3.1 กำหนดให้เส้นตรง EC เป็นระยะทางจากโลกถึงดวงจันทร์

           3.2 เส้น FE เป็นเส้นผ่าศูนย์กลางเงามืดของโลกที่ดวงจันทร์ต้องเคลื่อนตัวผ่านระหว่างปรากฏการณ์จันทรุปราคาเต็มดวง และเส้น ED เท่ากับเส้นผ่าศูนย์กลางของดวงจันทร์

           3.3 มุม FAE = มุม ECD เพราะเป็นสามเหลี่ยมรูปคล้าย จากการจับเวลา (เข้าใจว่าท่านใช้นาฬิกาทราย) การเคลื่อนตัวของดวงจันทร์ตั้งแต่เริ่มเข้าแตะเงามืดจนกระทั้งออกจากเงามืดทั้งดวง ท่าน "อรีสตาชัส" พบว่าขนาดของดวงจันทร์ (ED) กับเส้นผ่าศูนย์กลางเงามืด (FE) มีอัตราส่วน 1 : 2.5 หรือ ED : FE = 1 : 2.5 

          3.4 ในเมื่อสามเหลี่ยมทั้งสองรูป AFE กับ ECD เป็นสามเหลี่ยมรูปคล้าย เส้นตรง EC กับ AE จึงมีเป็นสัดส่วน EC : AE = 1 : 2.5 ในทำนองเดียวกัน EC + AE = 1 + 2.5 = 3.5 ดังนั้นจึงทำให้เส้นตรง AC มีความยาว = 3.5 ส่วน  ยังผลให้ EC = 1 ส่วน จากความยาวทั้งหมดของ AC 3.5 ส่วน

          3.5 ผลของการคำนวณจากข้อที่ 1. ทราบว่า AC = 864,000 ไมล์ (ความยาวเงามืดของโลก) ดังนั้น EC = 864,000 ไมล์ หารด้วย 3.5 ผลลัพท์ออกมาเป็น 240,000 ไมล์ หรือ 384,000 กิโลเมตร

          3.6 ท่าน "อรีสตาชัส" เมื่อสองพันกว่าปีที่แล้วสามารถคำนวณระยะทางจากโลกถึงดวงจันทร์ได้ตัวเลข 384,000 กิโลเมตร เมื่อเปรียบเทียบกับผลการคำนวณด้วยตัวช่วยสุดแสนไฮเทคอย่างดาวเทียมกับคอมพิวเตอร์รุ่นทันสมัยได้ตัวเลข 385,000 กิโลเมตร มีความคลาดเคลื่อนเพียง 0.26 % เท่านั้น

 

   

       ปฏิบัติการ "ราหูอมจันทร์" 15 เมษายน 2557 

          คราวนี้มาถึงหน้าที่ของผมในการคำนวณระยะทางจากโลกไปยังดวงจันทร์ คืนวันที่14 ต่อเนื่องถึง 15 เมษายน ภายใต้ปรากฏการณ์จันทรุปราคาเต็มดวง (total lunar eclipse) ผมอยู่ที่บ้านเมือง Broken Arrow รัฐ Oklhoma สหรัฐอเมริกา ทราบข้อมูลล่วงหน้าว่าจะดวงจันทร์เริ่มเข้าสู่เงามืดของโลก (Umbra) ตั้งแต่ 12:58 น. เวลาท้องถิ่น และจะสิ้นสุดเวลา 04:33 น. โดยเปรียบเทียบการจับเวลาด้วยนาฬิกาข้อมือของผมกับข้อมูลของสมาคมดารศาสตร์แห่งรัฐโอคลาโฮม่า สรุปได้ข้อยุติ ดังนี้ 

12:58 น. ดวงจันทร์เริ่มแตะเข้าเงามืด

02:06 น. ดวงจันทร์เข้าเงามืดหมดทั้งดวง

03:24 น. ดวงจันทร์เริ่มโผล่ออกจากเงามืด

04:33 น. ดวงจันทร์ออกจากเงามืดทั้งดวง  

 

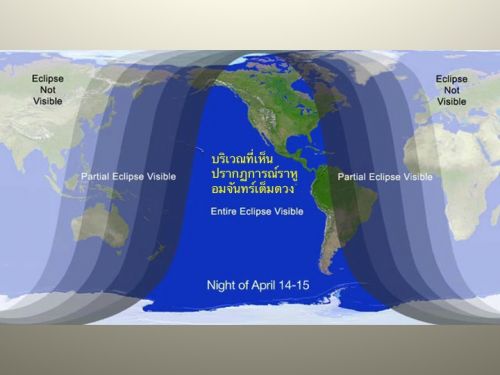
แสดงแผนที่บริเวณที่มองเห็น "จันทรุปราคาเต็มดวง" ในคืนวันที่ 14 - 15 เมษายน 2557 ได้แก่ทวีปอเมริกาเหนือ อเมริกากลาง และอเมริกาใต้ฝั่งตะวันตก กับเกาะต่างๆในมหาสมุทรแปซิฟิก

 

ทดสอบความพร้อมของกล้องถ่ายรูปเตรียม "ปฏิบัติการราหูอมจันทร์" ท่ามกลางอากาศหนาวจัดที่หน้าบ้าน เมือง Broken Arrow, Oklahoma State USA ที่นั่นเป็นคืนวันที่ 14 ต่อเนื่องถึง15 เมษายน เป็นฤดูใบไม้ผลิตกำลังจะย่างเข้าฤดูร้อนแต่อากาศก็หนาวจัดถึงอุณหภูมิติดลบ ปฏิบัติการราหูของผมจึงลำบากมากต้องวิ่งเข้าวิ่งออกตลอดเวลาเพราะทนหนาวนานๆไม่ไหวต้องเข้ามารับไออุ่นจากเครื่องทำความร้อนในตัวบ้านเป็นช่วงๆ ดีไม่ดีจะแข็งตายอยู่นอกบ้านกลายเป็นขึ้ปากชาวอเมริกันผิวดำที่คนไทยเรียกเขาว่า "พี่มืด" พวกเขาอาจจะวิจารณ์ในภาษาท้องถิ่นว่า "อยู่ดีไม่ว่าดี รนหาเรื่องเองนี่หว่า" (serve you guy right)   

 

 ผมใช้ข้อมูลการเคลื่อนตัวดวงจันทร์จากเว้ปไซด์ของสมาคมดาราศาสตร์แห่งรัฐโอคลาโฮม่า เพื่อสอบเทียบกับนาฬิกาข้อมือปรากฏว่ามีความใกล้เคียงกันมากต่างกันเพียงระดับวินาที

 

 

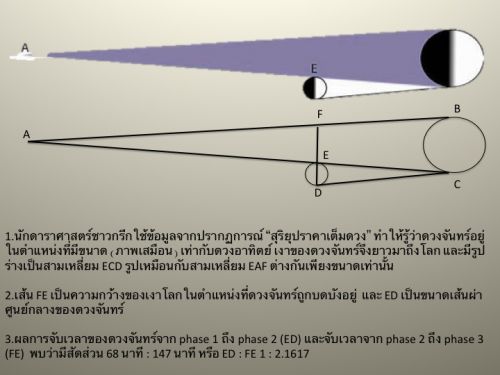
                   ใช้ข้อมูลในการคำนวณ ดังนี้

          1. ดวงจันทร์ เริ่มแตะเงามืด phase 1 เมื่อเวลา 12:58 น. และเข้าสู่เงามืดจนมิดทั้งดวง phase 2 เวลา 02:06 น. แสดงว่ากินเวลา 68 นาที หมายความว่าการเคลื่อนตัวเท่ากับความยาวเส้นผ่าศูนย์กลางของดวงจันทร์ใช้เวลา 68 นาที กำหนดให้ ED = 68 

          2. ดวงจันทร์ออกจากเงามืดทั้งดวง phase 3 เวลา 04:33 น. เมื่อคิดตวามต่างของเวลาระหว่างเข้าสู่เงามืดทั้งดวง phase 2 กับ phase 3 เท่ากับ 147 นาที กำหนดให้ FE = 147

          3. คิดสัดส่วน ED : FE = 68 : 147 ได้ผลลัพท์ 2.1617 

                4. นำสัดส่วน 1 : 2.1617 มาใช้กับ EC : AE จะได้สัดส่วนความยาว EC = 1 และ AE = 2.1617 ดังนั้นเส้น AC = EC + AE = 3.1617 และสัดส่วน EC : AC = 1 : 3.1617 

          5. ตามหลักฟิสิกซ์ดาราศาสตร์เงาของโลกในอวกาศ AC = 108 เท่าของเส้นผ่าศูนย์กลางของโลก ในที่นี้ใช้ข้อมูลการคำนวณเส้นรอบวงโลก 38,451 กม. จากปฏิบัติการ "อีราโต้สทีเนส" ระหว่างปราสาทภูเพ็ก สกลนคร ประเทศไทย กับปราสาทบายน เมืองเสียมราช ประเทศกัมพูชา เมื่อวันที่ 21 มีนาคม 2555 (อ่านรายละเอียดในคอลั่มเดียวกันนี้) เข้าสูตร 2PiR = 38,451 กม. ได้ความยาวเส้นผ่าศูนย์กลางโลก = 12,234 กม.

          6. ความยาวเงามืดของโลกเท่ากับ 108 x 12,234 = 1,321,272 กม. ในที่นี้ AC = 1,321,272 กม. ดังนั้น EC = 1,321,272 / 3.1617 = 417,899 กม. แสดงว่าจากปฏิบัติการราหูอมจันทร์ในค่ำคืนนี้ได้ค่า ระยะทางจากโลกไปดวงจันทร์ 417,899 กม.

               7. เปรียบเทียบกับระยะทางเฉลี่ยขององค์การนาซ่า 385,000 กม (mean distance) ความคลาดเคลื่อนของ "ปฏิบัติการราหูอมจันทร์" มีค่า 8.54 % แสดงว่าผมแพ้ท่าน Aristarchus of Samon 230 BC ที่มีค่าความคลาดเคลื่อนเพียง 0.26 %

          อนึ่งวงโคจรของดวงจันทร์ไม่ได้เป็นวงกลมเสียทีเดียว ทำให้ระยะทางจากโลกถึงดวงจันทร์มีส่วนที่ต่างกัน ดังนี้

          ระยะทางเฉลี่ย (mean distance) 385,000 Km

          ระยะใกล้ที่สุด (perigee) 356,400 - 370,400 Km

          ระยะไกลที่สุด (apogee) 404,000 - 406,700 Km

 

 

 

 

           นอกจากปัจจัยความคลาดเคลื่อนข้างต้นแล้ว ยังมีความคลาดเคลื่อนที่พัวพันมาจาก "ปฏิบัติการอีราโต้สทีเนส" ระหว่างปราสาทภูเพ็ก สกลนคร ประเทศไทย กับปราสาทบายน เมืองเสียมราช ประเทศกัมพูชา เมื่อวันที่ 21 มีนาคม 2554 ซึ่งมีความคลาดเคลื่อนของเส้นรอบวงโลกประมาณ 3.9% ดังนั้น ถ้านำความคลาดเคลื่อนของปฏิบัติการทั้งสองมารวมกันก็ยังผลให้เกิดความคลาดเคลื่อนใน "ปฏิบัติการราหู" ครั้งนี้อย่างที่ท่านเห็น 

           อย่างไรก็ตามถ้าผมจะแก้ตัวใหม่ก็ต้องไปปฏิบัติการที่ประเทศนิวซีแลนด์ หรือฝั่งตะวันตกของประเทศออสเตเรีย วันที่ 8 ตุลาคม 2557 หรือไม่ก็ต้องกลับมาที่บ้านอเมริกาอีกครั้งวันที่  28 กันยายน 2558 ผมตรวจดูตารางการเกิด "จันทรุปราคาเต็มดวง" แล้ว ประเทศไทยต้องรอไปถึงปี พ.ศ. 2561 (2018) ในปีนั้นพี่ไทยอย่างเราๆท่านๆจะได้ชม "ราหูอมจันทร์เต็มดวง" ถึงสองครั้ง 

          8 Oct 2014  New Zealand, East Australia, Alaska, Canada

              28 Sep 2015 North America, South America and Europe

          31 Jan 2018 Thailand

                28 July 2018  Thailand (เป็นฤดูฝนไม่แน่ใจว่าท้องฟ้าจะเปิดหรือไม่) 

 

ผมได้ประสานงานล่วงหน้ากับพรรคพวกที่เกาะทัสมาเนีย ประเทศออสเตเรีย ชื่อ Mr.Ken White พี่แกเป็นสมาชิกของสโมสรโรตารีสากลที่เมืองนั้น (เหมือนกับผมเป็นสมาชิกสโมสรโรตารีสากลที่สกลนคร) ผมได้ขอให้แกช่วยหานักดาราศาสตร์มาร่วมปฏิบัติการโดยถ่ายภาพและจับเวลาของดวงจันทร์ และส่งข้อมูลให้ผมทางอีเมล์ในคืนวันที่ 8 October 2014 ผมจะเข้าสูตรคำนวณอยู่ในหน้าจอคอมพิวเตอร์ที่สกลนคร ประเทศไทย นับว่าเป็นปฏิบัติการดาราศาสตร์ข้ามทวีปเป็นครั้งสำคัญ

 

ราหูจะเริ่มอมดวงจันทร์ตั้งแต่หัวค่ำเวลา19:53 น. วันที่ 31 มกราคม พ.ศ. 2561 และดวงจันทร์จะออกจากปากราหูกลับมาสว่างเต็มดวงอีกครั้งหนึ่งเวลา 21:07 น.

 

 ราหูจะเริ่มอมดวงจันทร์ตามเวลาในประเทศไทย 02:32 น. วันเสาร์ที่ 28 กรกฏาคม พ.ศ. 2561 และดวงจันทร์กลับมาสุกสว่างเต็มดวงอีกครั้งเวลา 04:13 น. อนึ่งวันดังกล่าวจะตรงกับ "เข้าพรรษา" พอดี 

 

 

อุปกรณ์อย่างง่ายๆที่จะใช้ในการคำนวณระยะทางจากโลกถึงดวงจันทร์ ในปรากฏการณ์ราหูอมจันทร์

 

 

           ผมหวังว่าเมื่อถึง ปี 2561 นักเรียนหลายคนคงอยากจะ "ปฏิบัติการราหูอมจันทร์" หรือ Operation Rahu 2018 แต่ก่อนจะถึงวันนั้นเราอาจต้องซ้อมมือกันก่อน เพื่อให้เกิดความพร้อม และทางที่ดีน่าจะเตรียมกล้องวิดีโอที่มีการบันทึกเวลา ถ่ายภาพการเคลื่อนที่ของดวงจันทร์ตั้งแต่ต้นจนจบเก็บไว้เพื่อฉายซ้ำและคำนวณย้อนหลังได้..........สวัสดีครับ