Operation Rahu Episode VI
How Far and How Big is the Moon
Partial Lunar Eclipse 8 August 2017
ปฏิบัติการราหูเพื่อการศึกษาแบบบูรณาการระหว่างวิทยาศาสตร์และสังคมศาสตร์ วัดระยะทางจากโลกไปดวงจันทร์และวัดขนาดของดวงจันทร์ ในปรากฏการณ์จันทรุปราคา 8 สิงหาคม 2560
.jpg)
ก่อนอื่นใคร่ขอขอบพระคุณนักคณิตศาสตร์และนักดาราศาสตร์ชาวกรีกเมื่อครั้งบรรพกาล 3 ท่าน ได้แก่ Pythagoras, Aristarchus และ Eratosthenes ที่ได้ส่งมอบมรดกความรู้อันล้ำค่าแก่มวลมนุษย์ ทำให้ผมได้ศึกษา ค้นคว้า และนำมาพัฒนาต่อยอดให้ทันยุคทันสมัย และเป็นที่มาของ "ปฏิบัติการราหู" รวม 6 ครั้ง (Operation Rahu Episode I - VI)
.jpg)
ความเป็นมา
จากการศึกษาผลงานของนักดาราศาสตร์ชาวกรีกโบราณ Aristarchus of Samon 310 - 230 BC ทำให้ทราบวิธีคำนวณระยะทางจากโลกไปดวงจันทร์และนำไปทดสอบด้วยตนเองเป็นครั้งแรกในปรากฏการณ์จันทรุปราคาเต็มดวงเมื่อวันที่ 15 เมษายน 2557 ที่รัฐ Oklhoma USA หลังจากนั้นได้พัฒนาสมการขึ้นมาใหม่โดยต่อยอดวิธีการของท่าน Aristarchus ให้เป็นระบบ digital โดยใช้ภาพถ่ายจันทรุปราคาเพียงภาพเดียว และได้ทดลองใช้งาน 3 ครั้ง วันที่ 8 ตุลาคม 2557 วันที่ 4 เมษายน 2558 และ 27 กันยายน 2558 ปรากฏว่า "สมการใหม่ระบบดิจิต้อล" ใช้งานได้ดีมีความเที่ยงตรงสูงและไม่มีอะไรยุ่งยาก อุปกรณ์ที่ใช้มีเพียงกล้องถ่ายรูปกับโปรแกรม PowerPoint บวกความรู้ดาราศาสตร์และคณิตศาสตร์ระดับมัธยม สามารถศึกษารายละเอียด Operation Rahu I - IV ได้ในเว้ปไซด์เดียวกันนี้ (www.yclsakhon.com)

โลโก้ของปฏิบัติการราหู Operation Rahu ทั้ง 4 ครั้ง

ปฏิบัติการราหู ครั้งที่ 5 เป็นการวัดระยะทาง โลก - ดวงอาทิตย์ เมื่อวันที่ 9 มีนาคม 2559
ทำไมจึงใช้ชื่อ "ปฏิบัติการราหู" (Operation Rahu)
เป็นสไตล์ของผมโดยส่วนตัวที่ชอบผสมผสานระหว่างวิทยาศาสตร์และสังคมศาสตร์ ทำให้ปฏิบัติการทุกครั้งต้องมีชื่อรหัสที่สะท้อน Story Behind อาจจะเป็นเรื่องราวจากวรรณคดี ประวัติศาสตร์ ความเชื่อ หรือเหตุการณ์อย่างใดอย่างหนึ่งซึ่งสอดคล้องกับปฏิบัติการนั้นๆ
Operation Rahu มาจากเรื่องราวของ "ราหูอมจันทร์" ตามความเชื่อในศาสนาฮินดูและพุทธมหายาน ซึ่งกล่าวถึงพิธีการกวนน้ำอมฤตของเหล่าเทวดาและอสูร แต่ถูกราหูแอบมาแย่งน้ำอมฤตไปกิน เทพจันทราและเทพสุริยาเห็นเหตุการณ์จึงร้องบอกพระวิศนุให้รีบขว้างจักรตัดคอราหูเพื่อเอาน้ำอมฤตคืน ทำให้ราหูเหลือเพียงส่วนหัวที่เป็นอมตะเพราะได้ลิ้มรสน้ำอมฤตไปส่วนหนึ่ง ราหูเกิดความแค้นต่อเทพจันทราและเทพสุริยาจึงพยายามหาโอกาสใช้ปากไล่งับเทพทั้งสอง เป็นที่มาของชื่อ "ราหูอมจันทร์" ท่านที่สนใจสามารถอ่านรายละเอียดในบทความ "ราหู....น้ำอมฤต.....สนามบินสุวรรณภูมิ" ของเว้ปไซด์เดียวกันนี้

ผู้หลักผู้ใหญ่ที่สร้างสนามบินสุวรรณภูมิและสนามบินพนมเป็ญได้สั่งการให้นำ "พิธีกวนน้ำอมฤต" ไปไว้ที่นั่นเพื่อเป็นศิริมงคล ทุกท่านที่เดินทางไปต่างประเทศผ่านสนามบินดังกล่าวจะต้องได้เห็นภาพแบบนี้และอดไม่ได้ที่จะถ่ายรูปเป็นที่ระลึก
มีประโยชน์ต่อ STEMS Education อย่างไร และทำไมจึงเชิญชวนโรงเรียนในภาคอีสานเข้าร่วมโครงการ
คำว่า STEMS Education หมายถึงการเรียนรู้เชิงบูรณาการระหว่างวิชา Science - Technology - Engineering - Mathematic - Social Science พูดง่ายๆก็คือการผสมผสานระหว่าง "วิทยาศาสตร์และสังคมศาสตร์" ดังนั้นนักเรียนที่จะเข้าร่วมปฏิบัติการครั้งนี้จะได้รับความรู้แบบผสมผสานระหว่างวิชาต่างๆอย่างจุใจ อีกทั้งเป็นปฏิบัติการดาราศาสตร์ในรูปแบบใหม่เกิดจาก "ความคิดนอกกรอบที่จับต้องได้" เพื่อสร้างแรงจูงใจให้นักเรียนมีความคิดสร้างสรรในการค้นหาความรู้ใหม่ๆด้วยตนเอง
เบื้องต้นมองหาโรงเรียนในภาคอีสานตอนบนและอีสานตอนล่างซึ่งมีระยะทางห่างกันมากกว่า 200 กิโลเมตร เพื่อจับคู่ปฏิบัติการ หรือคู่มิตรดาราศาสตร์ (Astronomical Partner) ดังนี้
คู่ที่ 1 โรงเรียนศรีบัวบานวิทยาคม อ.เมือง จ.นครพนม N 17.39 E 104.72 กับ โรงเรียนตาเบาวิทยา อ.ปราสาท จ.สุรินทร์ N 14.64 E 103.47 ระยะทาง 332 กิโลเมตร
คู่ที่ 2 โรงเรียนธาตุนารายณ์วิทยา อ.เมือง จ.สกลนคร N 17.19 E 104.08 กับ โรงเรียนตาเบาวิทยา อ.ปราสาท จ.สุรินทร์ N 14.64 E 103.47 ระยะทาง 290 กิโลเมตร
เหตุผลที่ต้องจับคู่โรงเรียนในภาคอีสานตอนบนและภาคอีสานตอนล่าง เนื่องจากจะต้องทำ "ปฏิบัติการอีราโต้สทีเนส วัดโลกทั้งใบด้วยไม้แท่งเดียว" (Operation Eratosthenes) ให้ได้ตัวเลข "เส้นรอบวงและเส้นผ่าศูนย์กลางของโลก" เพื่อนำไปเข้าสมการในปฏิบัติการราหู (Operation Rahu) คำนวณระยะทางจากโลกไปดวงจันทร์
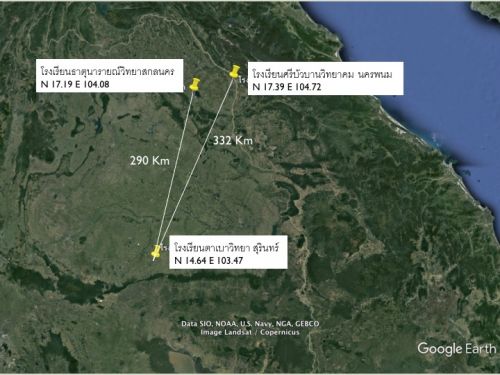
ตำแหน่งที่ตั้งของโรงเรียนทั้งสามแห่ง โรงเรียนศรีบัวบานวิทยาคม อำเภอเมืองจังหวัดนครพนม และโรงเรียนธาตุนารายณ์วิทยา อำเภอเมือง จังหวัดสกลนคร อยู่ภาคอีสานตอนบน ส่วนโรงเรียนตาเบาวิทยา อำเภอปราสาท จังหวัดสุรินทร์ อยู่ภาคอีสานตอนล่าง

ปฏิบัติการอีราโต้สทีเนส (Operation Eratosthenes) เป็นการคำนวณความยาวของเส้นรอบวงโลกโดยใช้ไม้แท่งเดียว
.jpg)
ราวสองพันกว่าปีที่แล้วนักดาราศาสตร์ชาวกรีก อีราโต้สทีเนส (Eratosthenes) ได้สร้างสมการคำนวณเส้นรอบวงโลกโดยใช้มุมดวงอาทิตย์ในปรากฏการณ์ครีษมายัน (Summer Solstice) และระยะทางระหว่างเมือง Alexandria - Syene ที่อาณาจักรอียิปส์
ขั้นตอนและวิธีการ
สูตรการวัดระยะทาง โลก - ดวงจันทร์ จำเป็นต้องใช้ตัวเลขเส้นผ่าศูนย์กลางของโลกเป็นข้อมูลเบื้องต้น ดังนั้นจึงต้องเริ่มด้วยการวัดเส้นรอบวงโลกโดย "ปฏิบัติการอีราโต้สทีเนส" (Operation Eratosthenes) และดัดแปลงเป็นเส้นผ่าศูนย์กลางด้วยสูตร 2Pai x radius
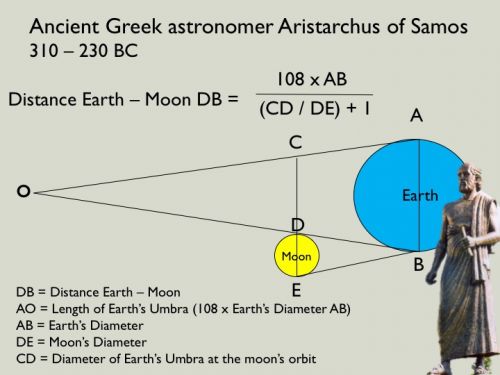
สูตรการคำนวณระยะทาง โลก - ดวงจันทร์ โดย Modified ให้เป็นระบบ Digital จากวิธีการดั้งเดิมของนักดาราศาสตร์ชาวกรีก Aristarchus of Samos เมื่อสองพันปีที่แล้ว สูตรนี้จำเป็นต้องใช้ตัวเลขเส้นผ่าศูนย์กลางของโลก (AB) เป็นพื้นฐาน
1.Operation Eratosthenes หาความยาวเส้นรอบวงโลกด้วยวิธีการของนักดาราศาสตร์ชาวกรีกโบราณ Eratosthenes วิธีการนี้ได้ปฏิบัติมาแล้วระหว่างปราสาทภูเพ็ก สกลนคร ประเทศไทย กับ ปราสาทบายน เสียมเรียบ ประเทศกัมพูชา เมื่อวันที่ 21 มีนาคม 2555 อ่านรายละเอียดได้ในบทความ "วัดโลกทั้งใบไทยกัมพูชา" เว้ปไซด์เดียวกันนี้ ในครั้งนี้เป็นการจับคู่ระหว่างโรงเรียนเพื่อคำนวณหาความยาวเส้นรอบวงโลก กำหนดดำเนินการตรงกับปรากฏการณ์ดาราศาสตร์ "ครีษมายัน" (Summer Solstice) กลางวันยาวที่สุดในรอบปี วันที่ 21 - 22 มิถุนายน 2560
วิธีคำนวณหาความยาวเส้นรอบวงโลก มี step ดังนี้
ทุกโรงเรียนทำ shadow plot เพื่อหามุมของดวงอาทิตย์ ณ เที่ยงสุริยะ (angle of the sun at solar noon) ให้เลือกวันใดวันหนึ่งระหว่างช่วง 20 - 26 มิถุนายน 2560 โดยมีช่วงเวลาปฏิบัติการระหว่าง 10:00 - 13:00 น.
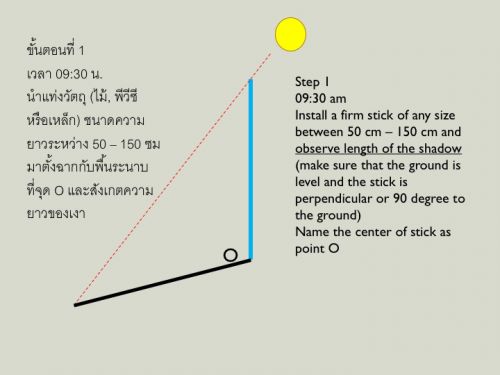
Step 1 หาที่โล่งๆและราบเรียบ เช่น สนามบาสเก็ตบอล สนามตะกร้อ ฯลฯ ติดตั้งอุปกรณ์ "แท่งไม้ พีวีซี เหล็ก ฯลฯ" ให้ตั้งฉากกับพื้นโดยให้เสร็จภายในเวลา 09:30 น. เริ่มต้นสังเกตความยาวของเงาที่ชี้ไปทางทิศตะวันตก
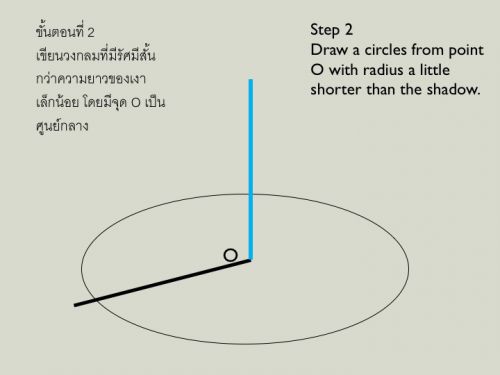
Step 2 สร้างวงกลมที่มีรัศมีสั้นกว่าเงาเล็กน้อย

Step 3 รอจนปลายเงาแตะวงกลม ทำสัญลักษณ์ A
.jpg)
Step 4 วัดความยาว OA และสร้างเส้นตรง OB = OA ไปแตะวงกลมฝั่งทิศตะวันออก
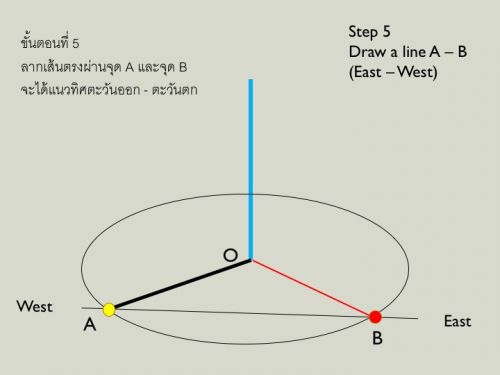
Step 5 ลากเส้นตรงผ่านจุด A และ B จะได้แนวทิศตะวันออก (B) - ตะวันตก (A)
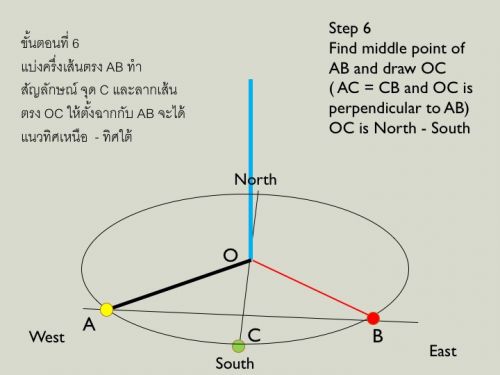
Step 6 จากจุด O ลากเส้นตรงให้ตั้งฉากกับ AB ซึ่งเป็นการแบ่งครึ่งทำให้ AC = CB และ OC คือแนวทิศเหนือ - ทิศใต้
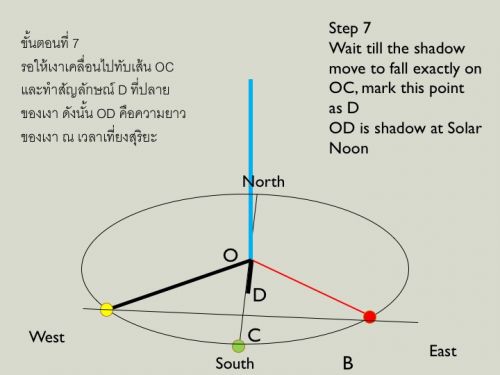
Step 7 รอให้เงาเคลื่อนมาทาบกับเส้นตรง OC ทำสัญลักษณ์ D ที่ปลายเงา OD คือเงาของแท่งไม้ ณ เที่ยงสุริยะ (Solar Noon)
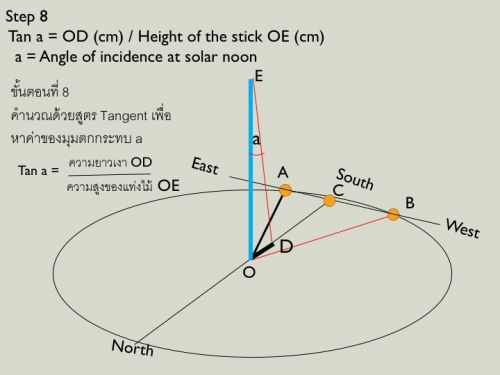
Step 8 คำนวณด้วย Tangent เพื่อหาค่าของมุมตกกระทบของดวงอาทิตย์ ณ เที่ยงสุริยะ (a)
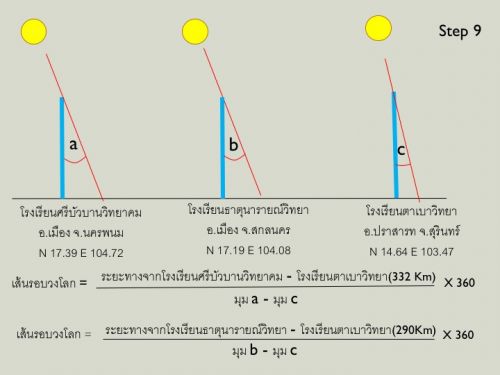
Step 9 คำนวณความยาวเส้นรอบวงโลกด้วยสูตร Eratosthenes ดังภาพ
อนึ่ง การหาค่ามุมตกกระทบของดวงอาทิตย์ ณ เที่ยงสุริยะ มีอีกหนึ่งวิธีเป็นการเรียนรัดใช้เวลาเพียงไม่เกิน 15 นาที เหมาะสำหรับผู้คนประเภท "บ้านไกลเวลาน้อย" ผมใช้โปรแกรมคอมพิวเตอร์กำหนดเวลาเก็บข้อมูลความยาวของเงา ณ เที่ยงสุริยะ และทำเป็นตารางให้ ดังนี้ (อย่างไรก็ตาม นักดาราศาสตร์ผู้ที่เป็นมืออาชีพจะไม่ชอบวิธีนี้เพราะมัน "หน่อมแน้ม" และเป็นการเอาเปรียบนักดาราศาสตร์เมื่อครั้งโบราณมากเกินไป ถ้าบรรพชนเหล่านั้นฟื้นขึ้นมาได้ ท่านคงจะชี้หน้าใส่พวกเราพร้อมกับพูดว่า "พวกสูมันแค่เด็กๆ" )
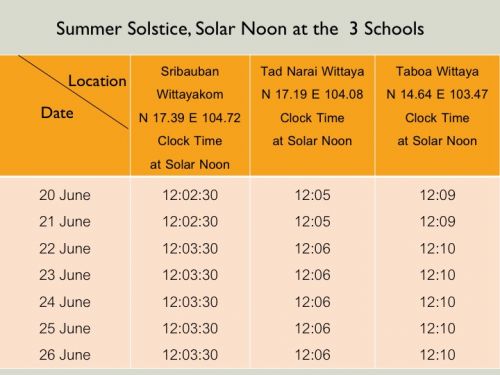
ตารางกำหนดเวลาวัดความยาวเงาของแท่งไม้ ณ เที่ยงสุริยะ ระหว่างวันที่ 20 - 26 มิถุนายน 2560 สำหรับ 3 โรงเรียน
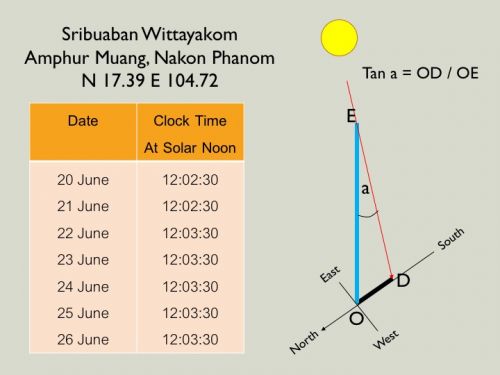
กำหนดเวลา "เที่ยงสุริยะ" (Solar Noon) โรงเรียนศรีบัวบานวิทยาคม นครพนม
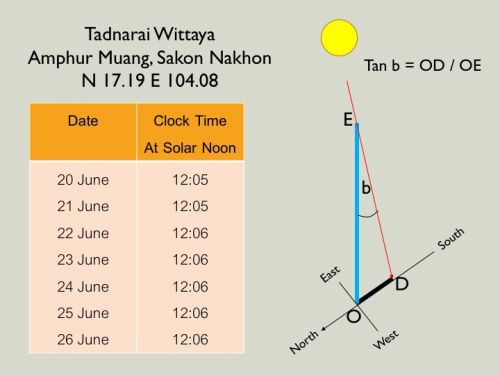
กำหนดเวลา "เที่ยงสุริยะ" (Solar Noon) โรงเรียนธาตุนารายณ์วิทยา สกลนคร
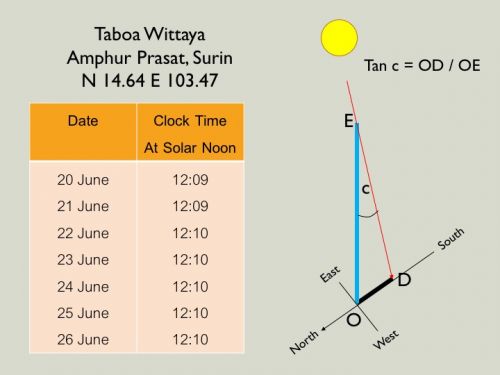
กำหนดเวลา "เที่ยงสุริยะ" (Solar Noon) ของโรงเรียนตาเบาวิทยา สุรินทร์
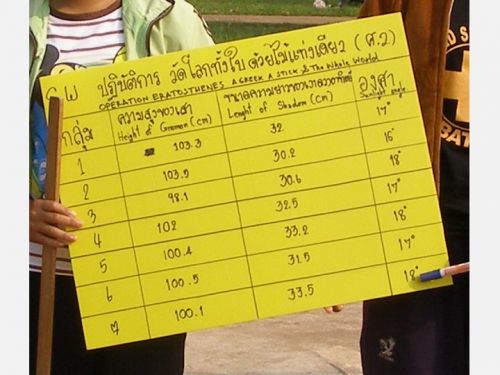
ตัวอย่าง "Operation Eratosthenes" ในรอบ 10 ปี ที่ผ่านมา เริ่มครั้งแรกที่โรงเรียนศรีบัวบานวิทยาคม อ.เมือง จ.นครพนมเมื่อวันที่ 23 กันยายน 2550 ประกบคู่กับโรงเรียนม่วงสามสิบอัมพวันวิทยา อ.ม่วงสามสิบ จ.อุบลราชธานี
.jpg)


.jpg)
ปฏิบัติการ Eratosthenes วัดโลกทั้งใบด้วยไม้แท่งเดียว ที่โรงเรียนศรีบัวบานวิทยาคม เมื่อวันที่ 23 กันยายน 2550

เด็กๆได้แสดงฝีมือด้วยตนเองในการคำนวณเส้นรอบวงโลกโดยใช้เงาดวงอาทิตย์
การอบรม Operation Eratosthenes ให้แก่คุณครูคณิตวิทย์ จัดโดยองการพิพิธภัณฑ์วิทยาศาสตร์แห่งชาติ (อพวช.)
.jpg)
องค์การพิพิธภัณฑ์วิทยาศาสตร์แห่งชาติ (อพวช) จัดหลักสูตร "ปฏิบัติการอีราโต้สทีเนส" วัดโลกทั้งใบด้วยไม้แท่งเดียว ให้แก่คุณครูมัธยมสายคณิต-วิทย์ รวม 4 รุ่น เริ่มครั้งแรก 22-23 กันยายน 2551
.jpg)
ในการอบรมปฏิบัติการอีราโต้สทีเนสที่ อพวช. มีทั้งบรรยายภาคทฤษฏีและภาคปฏิบัติในสนาม
เดินสายบรรยายเพื่อเตรียมความพร้อมและเก็บข้อมูลในการคำนวณเส้นรอบวงโลก 3 โรงเรียน
โรงเรียนตาเบาวิทยา อ.ปราสาท จ.สุรินทร์
วันที่ 5 มิถุนายน 2560 เตรียมความพร้อมกับนักเรียนมัธยม 6 โดยการจัดการของท่านผู้อำนวยการโรงเรียน ดร.ศักดิ์อนันต์ อนันตสุข

บรรยายให้กับนักเรียน ม.6 โรงเรียนตาเบาวิทยา วันที่ 5 มิถุนายน 2560

นักเรียนชั้นมัธยม 6 โรงเรียนตาเบาวิทยาเก็บข้อมูลมุมตกกระทบของดวงอาทิตย์เมื่อวันที่ 26 มิถุนายน 2560
โรงเรียนธาตุนารายณ์วิทยา
วันที่ 7 มิถุนายน 2560 บรรยายให้นักเรียน English Program M.4 M.5 และเก็บข้อมูลจริงวันที่ 21 มิถุนายน 2560

บรรยายเตรียมความพร้อมที่โรงเรียนธาตุนารายณ์วิทยาแก่นักเรียน English Program M.4 M.5

เก็บข้อมูลจริงโรงเรียนธาตุนารายณ์วิทยาตรงกับปรากฏการณ์ครีษมายัน (Summer Solstice) วันที่ 21 มิถุนายน 2560 (อนึ่งกล้องถ่ายรูปของผมตั้งค่าวันที่จากสหรัฐอเมริกา จึงปรากฏวันที่ช้ากว่าประเทศไทย 1 วัน)
โรงเรียนศรีบัวบานวิทยาคม นครพนม
บรรยายแก่นักเรียนชั้นมัธยม 6 และเก็บข้อมูลมุมตกกระทบของดวงอาทิตย์ วันที่ 22 มิถุนายน 2560

โรงเรียนศรีบัวบานวิทยาคม 22 มิถุนายน 2560
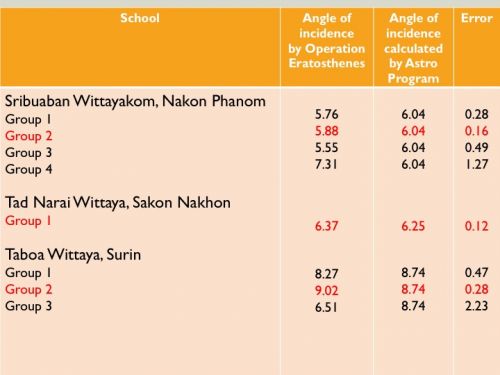
ข้อมูลมุมตกกระทบของดวงอาทิตย์ ณ เที่ยงสุริยะของทั้ง 3 โรงเรียน (ตัวสีแดงคือข้อมูลที่ใกล้เคียงกับโปรแกรมคอมพิวเตอร์ดาราศาสตร์มากที่สุด)
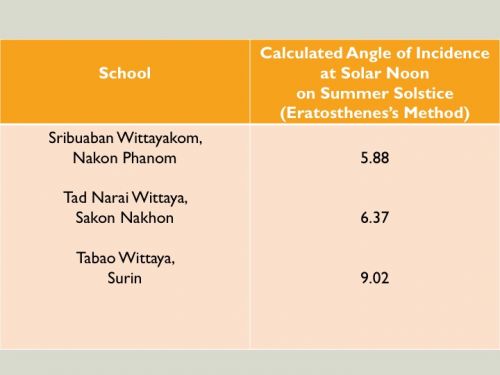
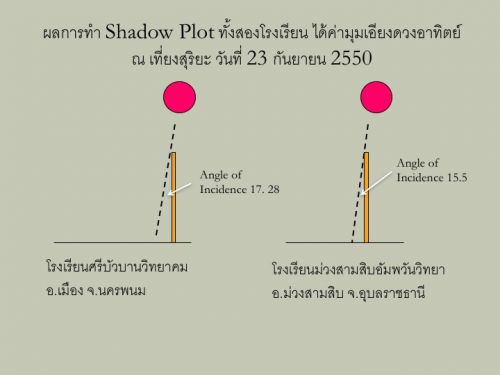
สรุปข้อมูลมุมตกกระทบของดวงอาทิตย์ (Angle of Incidence) ในปรากฏการณ์ "ครีษมายัน" วันที่ 21 - 26 มิถุนายน 2560 (Summer Solstice 21 - 26 June 2017) ณ เที่ยงสุริยะ (Solar Noon) ของทั้งสามโรงเรียน
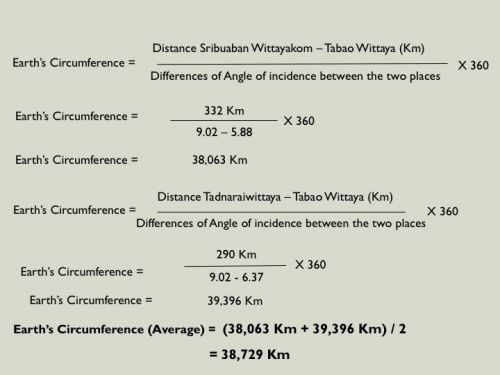
ผลการคำนวณเส้นรอบวงโลกภายใต้ "ปฏิบัติการอีราโต้สทีเนส" (Operation Eratosthenes 2017) ของโรงเรียนมัธยม 3 แห่ง ได้แก่ศรีบัวบานวิทยาคม นครพนม ธาตุนารายณ์วิทยา สกลนคร และตาเบาวิทยา สุรินทร์
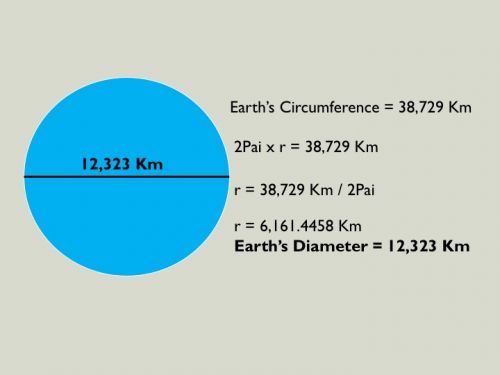
ผลการคำนวณ "เส้นผ่าศูนย์กลางของโลก" เท่ากับ 12,323 Km
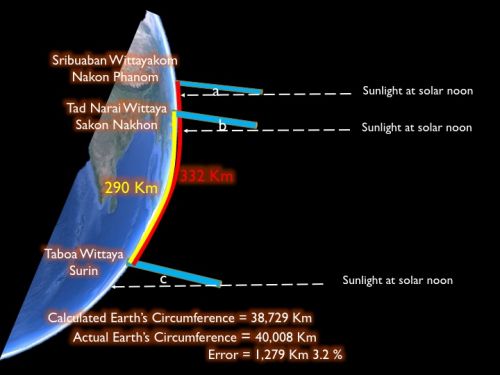
ปฏิบัติการ "อีราโต้สทีเนส" ได้ค่าเส้นรอบวงโลก 38,729 Km คาดเคลื่อน (Error) เพียง 3.2% จากตัวเลขเส้นรอบวงโลกจริงๆ 40,008 Km
2. ปฏิบัติการราหู (Operation Rahu) วัดระยะทางโลก - ดวงจันทร์ และขนาดของดวงจันทร์ คืนวันที่ 7 สิงหาคม 2560 จริงๆคือเวลา 0:03 - 02:18 ของวันที่ 8 สิงหาคม 2560 จะมีปรากฏการณ์ราหูอมจันทร์บางส่วน (partial lunar eclipse) มองเห็นได้ทั่วประเทศไทยและอีกหลายประเทศในทวีปเอเซีย อัฟริกา และออสเตเรีย สามารถใช้ภาพถ่ายของปรากฏการณ์นี้เข้าสมการระบบดิจิต้อลคำนวณระยะทางจากโลกไปดวงจันทร์ ดังตัวอย่างที่แสดงข้างล่าง
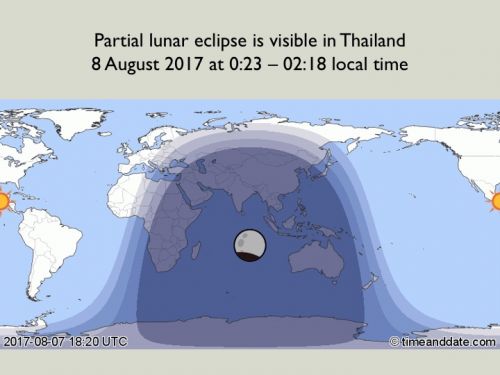
แผนที่แสดงประเทศต่างๆที่มองเห็นปรากฏการณ์ราหูอมจันทร์ ณ เวลาสากล GMT 18:20 วันที่ 7 August 2017 สำหรับประเทศไทยจะมองเห็นระหว่าง 0:23 - 02:18 วันที่ 8 สิงหาคม 2560

แผนผังแสดงปรากฏการณ์ราหูอมจันทร์บางส่วน (partial lunar eclipse) วันที่ 8 สิงหาคม 2560 ระหว่างเวลา 0:23 - 02:18

ถ่ายภาพราหูอมจันทร์ด้วยกล้องดิจิต้อลและเลือกภาพที่คมชัดที่สุดมาหนึ่งรูป เวลาที่เหมาะสมที่สุดน่าจะเป็น 01:20
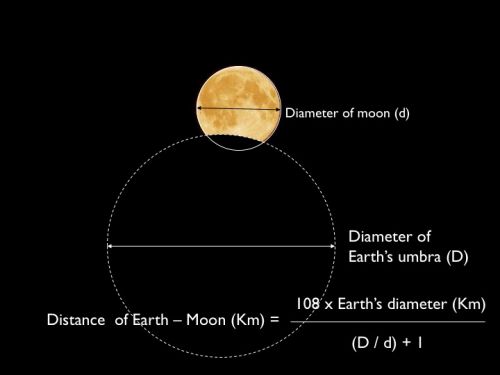
Download ภาพที่คัดเลือกว่าคมชัดมากที่สุดลงในโปรแกรม PowerPoint และใช้เทคนิคภาพเชิงซ้อนสร้างวงกลมเงามืดของโลก (Earth's Umbra) กับวงกลมของดวงจันทร์ เพื่อหาสัดส่วนของเส้นผ่าศูนย์กลาง (D / d) และเอาตัวเลขเส้นผ่าศูนย์กลางของโลกจากปฏิบัติการ Eratosthenes วันที่ 21 - 26 มิถุนายน 2560 มาเข้าสมการก็จะได้ระยะทางจากโลกไปดวงจันทร์ อย่างไรก็ตามขอให้นักเรียนเปรียบเทียบตัวเลขระยะทางจากโลกไปดวงจันทร์ที่ได้กับตัวเลขจริงๆจาก website ขององค์การ NASA มาดูว่ามีค่า % Error มากน้อยเพียงใด
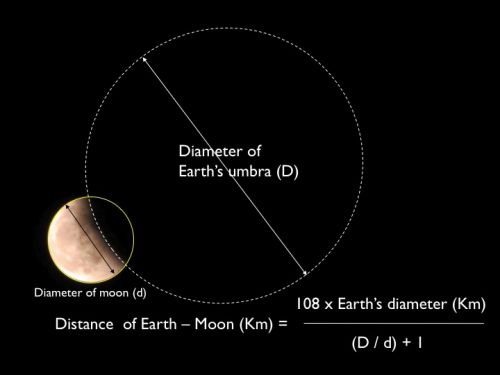
อีกหนึ่งตัวอย่างการคำนวณระยะทางจากโลกไปดวงจันทร์
ปฏิบัติการราหูจากภาพถ่ายจริงของปรากฏการณ์ "จันทรุปราคาบางส่วน"
คืนวันที 7 สิงหาคมต่อเนื่องถึงเช้าตรู่วันที่ 8 สิงหาคม 2560 ท้องฟ้าทั่วภาคอีสานมีเมฆมากและฝนฟ้าคะนองทั่วไปไม่สามารถถ่ายภาพดวงจันทร์ แต่โชคดีที่ได้ประสานกับมัคคุเทศก์อาชีพชื่อคุณ Pom Dararat ที่เชียงใหม่ซึ่งมีความรู้และมีฝีมือในการถ่ายภาพดาราศาสตร์ สามารถเก็บภาพ "ราหูอมจันทร์" ได้ชัดๆเพียงภาพเดียวเพราะที่นั่นก็มีเมฆมากเช่นกัน ภาพนี้เพียงพอต่อการทำ Simulation และเข้าสมการเป็นอย่างดีและมีผลดังนี้

ภาพราหูอมจันทร์เพียงใบเดียวที่คุณ Pom Dararat มัคคุเทศก์อาชีพที่เชียงใหม่ถ่ายได้อย่างสวยงาม ในคืนวันที่ 8 สิงหาคม 2560 เวลา 01:38 น.

นำภาพถ่ายราหูอมจันทร์มาเข้าโปรแกรม PowerPoint Simulation และเข้าสมการตามสูตร ใช้ตัวเลขเส้นผ่าศูนย์กลางของโลก (Earth's Diameter) จากปฏิบัติการอีราโต้สทีเนส 12,323 Km เป็นพื้นฐาน ได้ผลลัพท์ระยะทาง โลก - ดวงจันทร์ เท่ากับ 395,672 กม. คาดเคลื่อนจากตัวเลขของโปรแกรมคอมพิวเตอร์ดาราศาสตร์เพียง +1.5%

วัดขนาดเส้นผ่าศูนย์กลางของดวงจันทร์ได้เท่ากับ 3,664 Km คาดเคลื่อนเพียง + 5.5% (เส้นผ่าศูนย์กลางของดวงจันทร์ตามข้อมูลใน Google = 3,474 Km)
สรุป
ปฏิบัติราหู Operation Rahu น่าจะเป็นอีกหนึ่งแรงกระตุ้นให้นักเรียนได้เปิดมิติใหม่แห่งการเรียนรู้ด้วยการประยุกต์ความรู้พื้นฐานในเชิงบูรณาการระหว่างวิชาต่างๆทั้งวิทยาศาสตร์และสังคมศาสตร์ ซึ่งจะนำไปสู่การค้นพบมิติใหม่แห่งองค์ความรู้ด้วยตนเอง ..... ให้สมกับเราๆท่านๆอยู่ในยุค "ไทยก้มหน้า" Thailand 4.0
สรรค์สนธิ บุณโยทยาน
E-mail sansonthi@gmail.com



