ปฏิบัติการราหูภาค 5 วัดระยะทางโลก - ดวงอาทิตย์ (Operation Rahu Episode V)
ท่านผู้อ่านที่ติดตามผลงานของผมมาโดยตลอดคงทราบดีว่า "ปฏิบัติการราหู ภาค 1 - ภาค 4" (Operation Rahu Episode I - IV) เป็นการวัดระยะทางจากโลกไปดวงจันทร์ในปรากฏการณ์ "จันทรุปราคาเต็มดวง" ปฏิบัติการครั้งแรกเมื่อวันที่ 15 เมษายน 2557 ใช้สูตรดั้งเดิมของท่าน Aristarchus นักดาราศาสตร์ชาวกรีกโบราณเมื่อสองพันกว่าปีที่แล้ว ปฏิบัติการครั้งที่ 2 ถึงครั้งที่ 4 ได้พัฒนาต่อยอดสูตรของท่าน Aristarchus เป็นระบบดิจิต้อลใช้ภาพถ่ายชัดๆของราหูอมจันทร์เพียงรูปเดียวก็สามารถคำนวณระยะทางโลก - ดวงจันทร์ ได้ทันที อนึ่งการคำนวณในปฏิบัติการราหูจำเป็นต้องอาศัยตัวเลข "เส้นผ่าศูนย์กลางโลก" จาก "ปฏิบัติการอีราโต้สทีเนส ไทย - กัมพูชา" ซึ่งใช้มุมตกกระทบของดวงอาทิตย์ระหว่างปราสาทภูเพ็ก สกลนคร กับปราสาทบายน เมืองเสียมราช กัมพูชา รายละเอียดทั้งหมดนี้ท่านผู้อ่านสามารถเข้าชมได้ในบทความในเว้ปไซด์เดียวกันนี้

ปฏิบัติการอีราโต้สทีเนส วัดโลกทั้งใบไทย กัมพูชา เมื่อวันที่ 21 มีนาคม 2555 ได้ขนาดของโลกในรูปแบบเส้นรอบวงโลก และก็เส้นผ่าศูนย์กลางโลก

ปฏิบัติการราหู ครั้งที่ 1 - 4 วัดระยะทางโลก - ดวงจันทร์
วันที่ 9 มีนาคม 2559 เกิดปรากฏการณ์ "สุริยะคราส" (solar eclipse) ในมหาสมุทรแปซิฟิก โดยมีศูนย์กลางที่มองเห็นแบบ "เต็มดวง" (total solar eclipse) ที่ประเทศอินโดนีเซีย ส่วนบริเวณอื่นๆอย่างประเทศไทยและเพื่อนบ้านในแหลมทองจะมองเห็นแบบ "บางส่วน" (partial solar eclipse) ผมถือโอกาสทำปฏิบัติการดาราศาสตร์ภายใต้รหัส Operation Rahu Episode V เพื่อวัดระยะทางโลก - ดวงอาทิตย์ และวัดขนาดเส้นผ่าศูนย์กลางดวงอาทิตย์ในคราวเดียว

โลโก้ปฏิบัติการราหูภาค 5
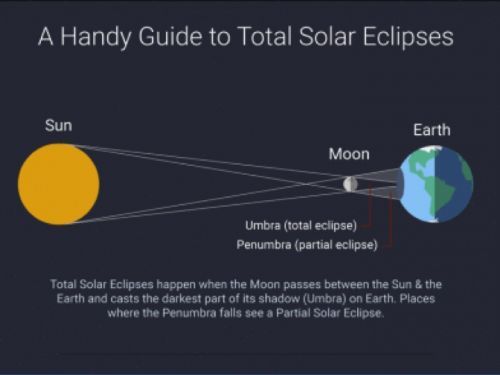
ไดอะแกรมแสดงการเกิดปรากฏการณ์ "สุริยะคราส"
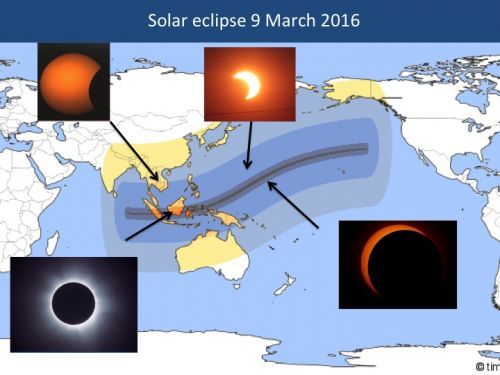
แผนที่แสดงเส้นทางของปรากฏการณ์ "ราหูอมสุริยะ" ในมหาสมุทรแปซิฟิก ประเทศอินโดนีเซียสามารถมองเห็นแบบเต็มดวง (total solar eclipse) ส่วนประเทศอื่นๆเช่น ประเทศไทย กัมพูชา และเวียดนาม มองเห็นได้แบบ "บางส่วน" (partial solar eclipse)
วิธีคำนวณระยะทางโลก - ดวงอาทิตย์
เทคโนโลยีต้นแบบของท่าน Aristarchus of Samos เมื่อสองพันกว่าปีที่แล้ว
เบื้องต้นผมต้องขอกราบขอบพระคุณองค์ความรู้ของนักดาราศาสตร์ชาวกรีกยุคสองพันกว่าปีที่แล้ว ท่าน Aristarchus of Samos เป็นต้นคิดโดยเริ่มจากการคำนวณระยะทางไปดวงจันทร์ได้ค่อนข้างแม่นยำ (รายละเอียดในปฏิบัติการราหูภาค 1) จากนั้นท่านก็พยายามคำนวณระยะทางจากโลกไปดวงอาทิตย์โดยใช้วิชาเรขาคณิต แม้ว่าผลการคำนวณครั้งนั้นจะไม่ถูกต้องแต่ท่านก็ได้วางรากฐานแห่งแนวคิดเอาไว้อย่างดียิ่ง ผลงานของท่านสร้างแรงดลใจให้ผมในการค้นคว้าและพัฒนาวิธีการคำนวณด้วยเทคโนโลยีในยุค 4G

Aristarchus of Samos 310 - 230 BC นักคณิตศาสตร์และดาราศาสตร์ในยุคกรีกโบราณ ใช้หลักเรขาคณิตและสูตร angular diameter คำนวณระยะทางโลก - ดวงอาทิตย์ ได้ประมาณ 18 - 20 เท่า ของระยะทางโลก - ดวงจันทร์ แม้ว่าตัวเลขนี้จะไม่ถูกต้องแต่ก็เป็น "หลักการต้นแบบ" ให้นักดาราศาสตร์ปัจจุบันนำมาใช้คำนวณอย่างแม่นยำมากขึ้น
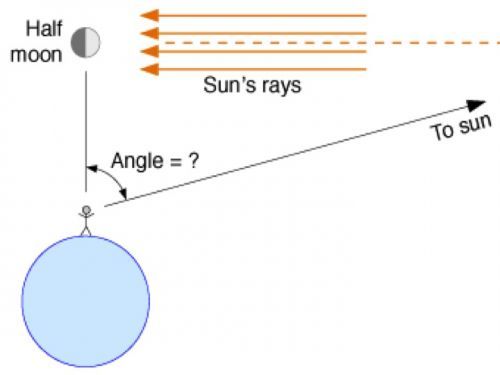
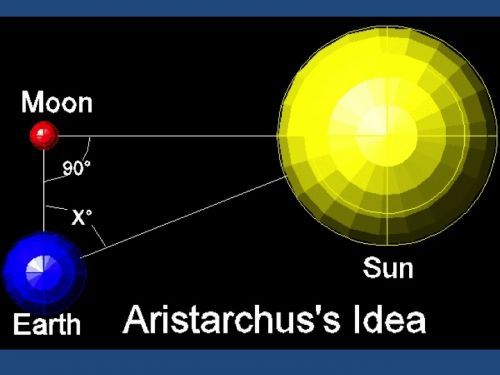
แนวคิดการคำนวณระยะทางโลก - ดวงอาทิตย์ ของท่าน Aristarchus โดยตั้งทฤษฏีว่าเมื่อดวงจันทร์โคจรเข้าสู่ตำแหน่งที่มองเห็น "ครึ่งดวง" ก็น่าจะตั้งฉากกับดวงอาทิตย์ ดังนั้นมุมที่ต่างกันระหว่างดวงจันทร์กับดวงอาทิตย์ (มุม X = 87 องศา) เมื่อเข้าสูตรเรขาคณิตในทฤษฏีสามเหลี่ยมมุมฉากจะได้ระยะทางโลก - ดวงอาทิตย์ ระหว่าง 18 - 20 เท่าของระยะทางโลก - ดวงจันทร์ อย่างไรก็ตามเป็นการยากมากถึงมากที่สุดสำหรับสายตามนุษย์ธรรมดาเมื่อสองพันกว่าปีที่แล้วในการวัดค่ามุมระหว่างตำแหน่งดวงจันทร์กับดวงอาทิตย์ ปัจจุบันนักวิทยาศาสตร์ใช้อุปกรณ์ไฮเทคสามารถวัดค่ามุม X ได้อย่างถูกต้องที่ตัวเลข 89 องศา 51 ลิปดา และทราบระยะทางโลก - ดวงอาทิตย์ เท่ากับ 400 เท่าของระยะทางโลก - ดวงจันทร์
ในยุคของท่าน Aristarchus เมื่อสองพันกว่าปีที่แล้วต้องใช้วิธีธรรมชาติที่เรียกว่า "ตาดู หูฟัง" ในการวัดมุมระหว่างดวงจันทร์กับดวงอาทิตย์ ท่านจึงวัดมุมดังกล่าวได้ 87 องศา คิดเป็นค่า Tan 87 = 19.08113669 (say 19) ดังนั้นสัดส่วนระหว่างระยะทาง โลก - ดวงจันทร์ : ME / MS = 1 / 19 อย่างไรก็ตามในยุคปัจจุบันเรามีเครื่องมือไฮเทคที่สามารถวัดมุมระหว่างดวงจันทร์กับดวงอาทิตย์อย่างแม่นยำ จึงได้ค่า 89.85 องศา คิดเป็นค่า Tan 89.85 = 381.97099076 และเพื่อให้เป็นตัวเลขที่ง่ายจึงปัดเป็น 400 สัดส่วน ME / MS = 1 / 400
.jpg)

ปฏิบัติการราหู ภาค 5 ในปรากฏการณ์ "สุริยะคราส" 9 มีนาคม 2559
มีขั้นตอนดังต่อไปนี้
1.หาขนาดของเส้นผ่าศูนย์กลางโลก (Earth's diameter) จาก "ปฏิบัติการอีราโต้สทีเนส" ปราสาทภูเพ็ก สกลนคร กับปราสาทบายน เมือง Siem Reap กัมพูชา เมื่อวันที่ 21 มีนาคม 2555 (Operation Eratosthenes 21 March 2012) ได้ค่าเส้นรอบวงโลก 38,451 กิโลเมตร และเส้นผ่าศูนย์กลางโลก 12,234 กิโลเมตร (อ่านรายละเอียดบทความปฏิบัติการอีราโต้สทีเนส ในเว้ปไซด์เดียวกันนี้)
.jpg)
2.หาค่าเฉลี่ยระยะทาง โลก - ดวงจันทร์ จาก Operation Rahu Episode I - Episode IV ได้เท่ากับ 404,717 กม. (Error 5.12%) และเส้นผ่าศูนย์กลางดวงจันทร์ 3,747 กม.
.jpg)
ผลของ Operation Rahu Episode I - IV ได้ค่าเฉลี่ยระยะทาง โลก - ดวงจันทร์ 404,717 กม.
.jpg)
ค่าเฉลี่ยของขนาดเส้นผ่าศูนย์กลางดวงจันทร์เท่ากับ 3,747 กม.ได้มาจากปรากฏการณ์สุริยุปราคา (Solar Eclipse) ที่เงาของดวงจันทร์ยาวมาถึงโลกเท่ากับระยะทาง โลก - ดวงจันทร์ ทำให้สามารถคำนวณย้อนกลับไปหาขนาดเส้นผ่าศูนย์กลางของดวงจันทร์โดยใช้สูตร (ระยะทางโลก - ดวงจันทร์) หารด้วย 108 (ตัวเลข 108 มาจากสูตรของกรีกโบราณที่กล่าวว่า ความยาวของเงาวัตถุทรงกลมเท่ากับ 108 เท่า ของเส้นผ่าศูนย์กลางของวัตถุนั้นๆ)

Logo Operation Rahu Episode I - IV
3. คำนวณระยะทาง โลก - ดวงอาทิตย์
ขณะที่เกิดปรากฏการณ์สุริยะปราคาบางส่วนที่ประเทศไทย (Partial Solar Eclipse) 9 มีนาคม 2559 ผมอยู่ที่ Tulsa USA จึงต้องขอความอนุเคราะห์จากมัคคุเทศก์อาชีพ ชื่อ facebook ว่า Pom Dararat ที่จังหวัดเชียงใหม่ประกบติดแบบยกต่อยกกับทีมงานสถาบันวิจัยดาราศาสตร์แห่งชาติ (National Astronomical Research Institute of Thailand: NARIT) ชมรมพรานดารา และ Centralfestival ตั้งแต่เช้ามืดวันที่ 9 มีนาคม 2559 (ผมเดินทางมาที่บ้านของลูกสาวในรัฐ Oklahoma สหรัฐอเมริกา ตั้งแต่วันที่ 7 มีนาคม 2559 ก็ต้องขอบคุณ social media facebook ที่ทำให้สามารถสื่อสารข้ามทวีปได้อย่างรวดเร็ว)

สถาบันวิจัยดาราศาสตร์แห่งชาติ จัดนิทรรศการขนาดย่อมและติดตั้งกล้องถ่ายภาพดวงอาทิตย์บนดาดฟ้า (เข้าใจว่าเป็นตึกของ Central festival) เช้ามืดวันที่ 9 มีนาคม 2559 จังหวัดเชียงใหม่

ภาพแรกที่ได้รับจากไกด์ Pom Dararat

ไกด์ Pom Dararat เป็นพรีเซนเตอร์ทำท่ายกดวงอาทิตย์ด้วยมือ

จากนั้นก็ได้รับภาพเพิ่มเติมจากไกด์ Pom Dararat และ ไกด์ Oh Prapangkornsuwaan ที่เชียงใหม่ และเลือกภาพที่ชัดที่สุดมาลงในโปรแกรม PowerPoint และ proceed ตามขั้นตอนของการทำภาพเชิงซ้อน


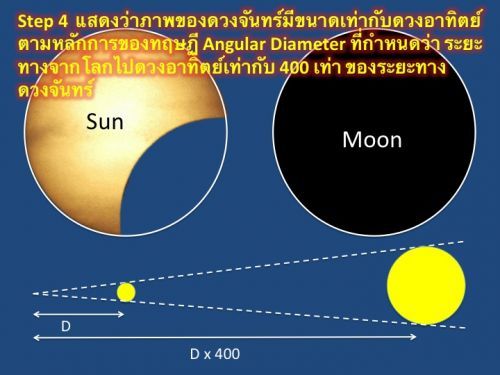
ผมเรียกทฤษฏี angular diameter ในสำนวนไทยว่า "เส้นผมบังภูเขา" หมายถึงภาพของดวงจันทร์สามารถบังดวงอาทิตย์ได้อย่างพอดีถ้ามองจากโลก ดังนั้นตามทฤษฏี angular diameter ระยะทางจากโลก - ดวงอาทิตย์ ย่อมเท่ากับ 400 เท่าของระยะทางโลก - ดวงจันทร์

ภาพถ่าย "สุริยะคราสแบบเต็มดวง" จากประเทศอินโดนีเซีย เป็นการยืนยันทฤษฏี angular diameter หรือเรียกแบบไทยๆว่า "เส้นผมบังภูเขา" ที่มีความหมายว่าดวงจันทร์เล็กกว่าดวงอาทิตย์หลายเท่าแต่ก็สามารถบดบังดวงอาทิตย์ได้อย่างมิดชิดพอดีในมุมมองจากโลก นักดาราศาสตร์ยุคปัจจุบันใช้วิธีนี้คำนวณว่าระยะทางโลก - ดวงอาทิตย์ เท่ากับ 400 เท่าของระยะทางโลก - ดวงจันทร์ ขณะเดียวกันขนาดดวงอาทิตย์ก็ใหญ่เท่ากับ 400 เท่าของดวงจันทร์
ผลการคำนวณ
1.ระยะทางโลก - ดวงอาทิตย์ = 400 x 404,717 กม. (ระยะทางโลก - ดวงจันทร์)
= 161,886,800 กม. หรือ 161.88 ล้าน กม.
(ระยะทางโลก - ดวงอาทิตย์ โดยเฉลี่ยจาก Google = 149.6 ล้าน กม. ดังนั้น Operation Rahu V มีค่า Error = 8.2%)
2.ขนาดของดวงอาทิตย์เท่ากับ 400 x 3,747 กม.(ขนาดเส้นผ่าศูนย์กลางของดวงจันทร์) เท่ากับ 1,498,800 กม.
หมายเหตุ
ค่า Error 8.2% มาจากการสะสมความคลาดเคลื่อนตั้งแต่
1.การคำนวณขนาดเส้นผ่าศูนย์กลางโลก
2.การคำนวณระยะทางโลก - ดวงจันทร์
3.ค่าเฉลี่ยตามสูตร angular diameter ที่ปรับจาก 381.970 เป็นตัวเลขกลมๆที่ 400 ถ้วนๆ
อย่างไรก็ตามหากเลือกหยิบเอาตัวเลขที่ Error น้อยที่สุด (0.3%) ของระยะทางโลก - ดวงจันทร์ 386,224 กม. จาก Operation Rahu Episode II และใช้ค่า angular diameter 381.970 จะได้ระยะทางโลก - ดวงอาทิตย์ เท่ากับ 147.52 ล้าน กม. มีค่า Error เพียง 1.4% (ระยะทางเฉลี่ย โลก - ดวงอาทิตย์ 149.6 ล้าน กม.)
สรุป
ปฏิบัติการราหูภาค 5 ในปรากฏการณ์สุริยะคราส 9 มีนาคม 2559 เป็นการคำนวณระยะทางโลก - ดวงอาทิตย์ ด้วยเทคโนโลยีใหม่แห่งยุค 4G โดยนำหลักการของนักดาราศาสตร์ชาวกรีก ท่าน Aristarchus of Simon เมื่อสองพันกว่าปีที่แล้วมาพัฒนาต่อยอด และก็ต้องอิงข้อมูลจาก "ปฏิบัติการอีราโต้สทีเน้ส ไทย - กัมพูชา" และปฏิบัติการราหูภาค 1 - 4 เป็นตัวเลขตั้งต้น ดังนั้นปฏิบัติการดาราศาสตร์ของผมแทบทุกครั้งจะมีความเชื่อมโยงระหว่างกันในลักษณะ "สมการต่อเนื่อง" หวังว่าสิ่งต่างๆที่ได้ทำจะเป็นตัวอย่างหนึ่งของการสร้างแนวคิดในเชิงวิชาการให้แก่นักเรียนและนักศึกษา



