Operation Rahu Episode II Calculate Earth-moon distance with the help of "one photo" 

ปฏิบัติการราหู ภาคสอง พบสูตรใหม่.....คำนวณระยะทางจากโลกไปดวงจันทร์.....ด้วยภาพถ่ายเพียง 1 ภาพ

 

 

           เป็นการร่วมมือข้ามทวีประหว่างสกลนคร ประเทศไทย กับเมือง Hobart เกาะ Tasmania ประเทศ Australia ใช้ภาพถ่าย "ราหูอมจันทร์" จากสองสถานที่เข้าโปรแกรมภาพเชิงซ้อนเพื่อหาสัดส่วนระหว่างเส้นผ่าศูนย์กลางของเงาโลก (Earth's umbra) และเส้นผ่าศูนย์กลางของดวงจันทร์ (Moon's diameter) และเข้าสมการกับ "เส้นผ่าศูนย์กลางของโลก" (Earth's diameter) จากผลของปฏิบัติการอีราโต้สทีเนส ระหว่างปราสาทภูเพ็ก สกลนคร ประเทศไทย กับปราสาทบายน เสียนมราช ประเทศกัมพูชา (Operation Eratosthenes 2012) เมื่อวันที่ 21 มีนาคม 2555 ...........สามารถคำนวณระยะทางจากโลกไปดวงจันทร์ได้อย่างค่อนข้างแม่นยำ ด้วยสูตรคณิตศาสตร์ง่ายๆ

 

 

สมการคำนวนระยะทาง โลก - ดวงจันทร์ ด้วยภาพถ่ายปรากฏการณ์ราหูอมจันทร์

 

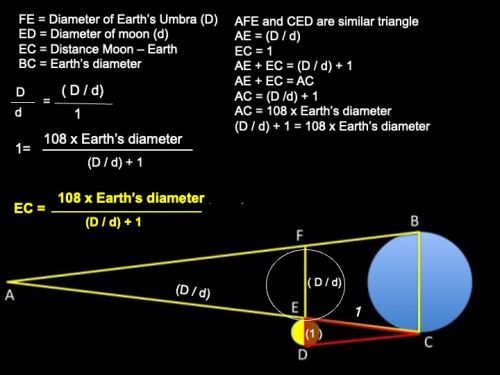
ที่มาของสมการวัดระยะทาง โลก - ดวงจันทร์

 

           ก่อนอื่นผมต้องขอแสดงความคารวะต่อภูมิปัญญาของบรรพชนชาวกรีกเมื่อสองพันกว่าปีที่แล้ว ได้แก่ท่าน Pythagoras ท่าน Eratosthenes และท่าน Aristarchus of Simon  ที่ได้ถ่ายทอดความรู้ดาราศาสตร์และคณิตศาสตร์ไว้ให้ผมได้ศึกษาและนำมาประยุกต์ใช้ในปัจจุบัน ได้นำวิธีการของท่านเหล่านี้มาต่อยอดด้วยเทคโนโลยีของกล้องถ่ายรูประบบดิจิต้อลและโปรแกรมคอมพิวเตอร์ PowerPoint ทำให้สามารถคำนวณได้ง่ายขึ้น ถ้าท่านเหล่านั้นฟื้นขึ้นมาได้ก็คงจะพูดว่า "สูเจ้าเล่นเอาเปรียบตูข้านี่หว่า สมัยของข้ามีแต่วิธี ตาดู หูฟัง และจับเวลาด้วยนาฬิกาทราย"

      อย่างไรก็ตามผมได้เขียน "ปฏิบัติการราหู ภาคหนึ่ง" ซึ่งทำเมื่อวันที่ 15 เมษายน 2557 ที่เมือง Broken Arrow รัฐ Oklahoma ประเทศสหรัฐอเมริกา ท่านสามารถเข้าไปชมได้เว้ปเดียวกันนี้ ผมบรรยายไว้อย่างละเอียดว่าทำไมต้องใช้ชื่อปฏิบัติการครั้งนี้ว่า "ราหู" มีที่มาอย่างไรทั้งด้านนิทาน ตำนาน และดาราศาสตร์

          หลักการที่ใช้ในการคำนวณ

                   ก. ชาวกรีกทราบมานานแล้วจากพื้นฐานคณิตศาสตร์ว่า เงาของโลกยาวเท่ากับ 108 เท่าของเส้นผ่าศูนย์กลาง ดังนั้นเมื่อเส้นผ่าศูนย์กลางของโลก = 12,234 กิโลเมตร (ข้อมูลจากปฏิบัติการ Operation Eratosthenes 21 March 2012) ความยาวของเงาโลกมีลักษณะ cone shape 108 x 12,234 Km = 1,321,272 Km  

 

                   

 

                  ข. เงาของดวงจันทร์ก็มีคุณสมบัติเช่นเดียวกับเงาของโลก คือ 108 เท่าของเส้นผ่าศูนย์กลาง และจากปรากฏการณ์สุริยุปราคา (solar eclipse) เงาของดวงจันทร์ก็ตกมาถึงผิวโลกในลักษณะ cone shape ดังนั้น เงาของโลกและเงาของดวงจันทร์จึงเป็น "สามเหลี่ยมคล้าย"

 

                 

 

                 

 

           

 

                ค. ท่าน Aristarchus นักดาราศาสตร์ชาวกรีกผู้ค้นพบวิธีการคำนวณระยะทาง โลก - ดวงจันทร์ ด้วยวิธีการนับเวลาการเคลื่อนที่ของดวงจันทร์ผ่านเงามืดของโลก เพราะทราบดีว่าดวงจันทร์ต้องอยู่ที่ใดที่หนึ่งภายในระยะเงามืดของโลก หากดวงจันทร์อยู่ไกลออกไปพ้นเงามืดของโลกก็จะไม่มีปรากฏการณ์ "จันทรุปราคาเต็มดวง" และหากดวงจันทร์อยู่ปลายเงามืดในส่วนที่เล็กกว่าขนาดของดวงจันทร์จะมีเพียงปรากฏการณ์ "จันทรุปราคาบางส่วน"  

 

                   

 

                  

 

                

 

                  ท่าน Aristarchus นับเวลาเมื่อดวงจันทร์เริ่มแตะขอบของเงามืด A และนับเวลาดวงจันทร์หายไปไปในเงามืดจนหมดทั้งดวง B จากนั้นรอนับเวลาดวงจันทร์เคลื่อนพ้นเงามืดทั้งหมด C เวลาที่นับได้ทั้งหมด 3 ครั้ง เมื่อแปลงหน่วยเป็น "ระยะทาง" จะได้สัดส่วน "ขนาดของดวงจันทร์ กับขนาดเงามืดของโลก"

           ตามภาพไดอะแกรม

           ถ้ากำหนดให้ FE เป็นเส้นผ่าศูนย์กลางของเงามืด (D) และ ED เป็นเส้นผ่าศูนย์กลางของดวงจันทร์ (d)

                   FE : ED = D : d 

                   อีกนัยหนึ่ง D/d : 1 

                   เนื่องจาก FAE กับ ECD เป็นสามเหลี่ยมคล้าย ดังนั้น AE : EC = D/d : 1 

                   AC = D/d + 1 

                  AC or (D/d + 1) = ความยาวของเงาโลก (108 x เส้นผ่าศูนย์กลางโลก)

                    1 = (108 x เส้นผ่าศูนย์กลางโลก) / (D/d + 1) 

                     ระยะทาง โลก - ดวงจันทร์ = (108 x เส้นผ่าศูนย์กลางโลก) / (D/d +1) 

           

 

               

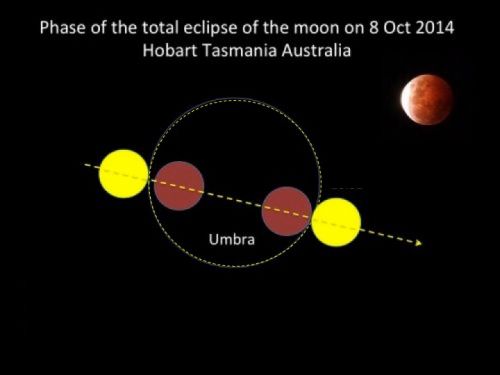
          1. ถ่ายภาพดวงจันทร์ในขณะที่อยู่ระหว่างเคลื่อนตัวเข้าเงามืด (umbra) หรือเคลื่อนตัวออกจากเงามืดของโลก ภาพนี้ดวงจันทร์กำลังเคลื่อนตัวออกจากเงามืด (ถ่ายจากบ้านที่สกลนคร คืนวันที่ 8 ตุลาคม 2557) จะเห็นภาพดวงจันทร์ถูกเงามืดกินเป็นรูปโค้งซึ่งเป็นส่วนหนึ่งของเงามืดทั้งหมด (เงามืดของโลกมีลักษณะเป็นวงกลม) 

 

 

 

2. ถ้าเอาวงเวียนหรือโปรแกรมการสร้างวงกลมใน PowerPoint เข้าไปเทียบเพื่อแนบให้สนิทกับรอยโค้ง จะได้วงกลมที่สมบูรณ์ของเงามืด (umbra) ทำแบบเดียวกันก็จะได้วงกลมที่สมบูรณ์ของดวงจันทร์เช่นกัน 

 

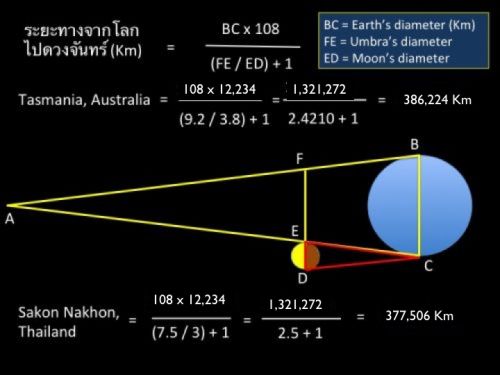
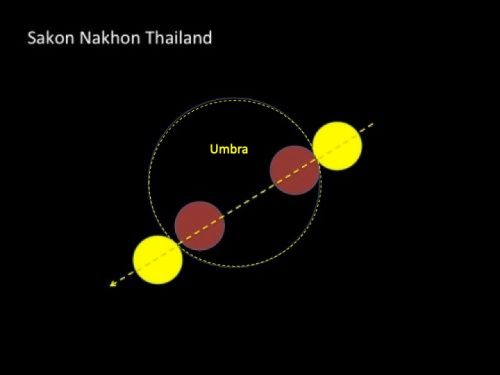
3. วัดความยาวเส้นผ่าศูนย์กลางของทั้งสองวงกลม เป็นหน่วยอะไรก็ได้แล้วนำมาเปรียบเทียบเป็นสัดส่วนโดยเอาเส้นผ่าศูนย์กลางของ umbra เป็นตัวตั้งแล้วหารด้วยเส้นผ่าศูนย์กลางของดวงจันทร์ ปฏิบัติการครั้งนี้มีการถ่ายภาพทั้งที่สกลนคร ประเทศไทย และที่เมือง Hobart เกาะ Tasmania ประเทศ Australia จะได้ตัวเลขของสกลนคร 7.5 / 3 = 2.5 Unit และ Australia 9.2 / 3.8 = 2.4210 Unit  (อนึ่งคำว่าสัดส่วนเป็นตัวเลขโดดๆที่ยังไม่ระบุหน่วย) ต้องขอขอบคุณเพื่อนชาวออสเตเรีย Mr.Ken White and Ms.Christine White และ Mr.Reg Travers ที่อดหลับอดนอนช่วยถ่ายภาพราหูอมจันทร์จนดึกดื่น 

 

ข้อมูลจากสกลนคร สัดส่วนระหว่าง Earth's umbra : Moon's diameter = 7.5 : 3 ( 2.5 : 1)  D = 2.5 d = 1 

 

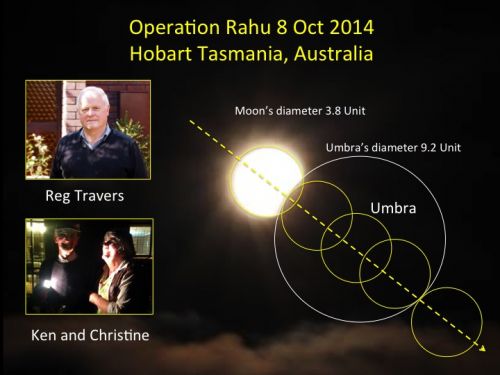
ข้อมูลจาก Tasmania Australia สัดส่วนระหว่าง Earth'sumbra : Moon's diameter 9.2 : 3.8 or 2.421:1 D = 2.421 d = 1 

 

 4. นำสัดส่วน 2.5 unit มาเข้าสมการดังภาพข้างล่าง อนึ่งข้อมูลตัวเลขที่จะใช้ในสมการนี้จะมาจากขนาดเส้นรอบวงของโลกซึ่งได้จาก "ปฏิบัติการอีราโต้สทีเนส เมื่อวันที่ 21 มีนาคม 2012" (ดูรายละเอียดในบทความนี้อยู่ในเว้ปเดียวกัน) และตัวเลขความยาวเงามืดของโลก (lenght of Earth's umbra) ซึ่งเท่ากับ 108 เท่าของเส้นผ่าศูนย์กลางของโลก (อ้างอิงมาจากภูมิปัญญาของบรรพชนชาวกรีกเมื่อสองพันกว่าปีที่แล้ว) 

 

 

 

สมการนี้เป็นการดัดแปลงมาจากภูมิปัญญาการคำนวณของท่าน Aristarchus of Simon เมื่อสองพันกว่าปีที่แล้ว ผมทำเป็นรูปแบบคณิตศาสตร์ให้สามารถใช้งานได้ง่ายขึ้น

 

 

 

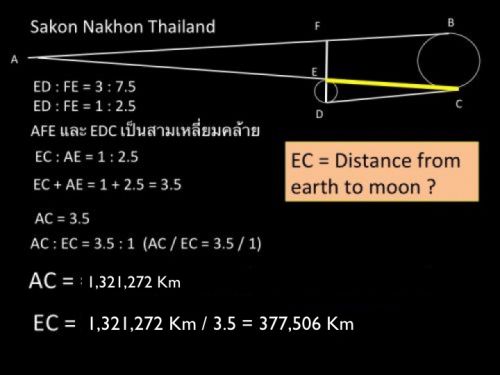
 5. ถอดสมการดังกล่าวตามสูตรจะได้ระยะทางจากโลกไปดวงจันทร์ ผลของการคำนวณที่สกลนครได้ ระยะทางเท่ากับ 377,506 Km คลาดเคลื่อน (error) 1.9% ส่วนการคำนวณจากภาพถ่ายที่ส่งมาจากออสเตเรีย ได้ 386,224 Km คลาดเคลื่อน (error) 0.3% จากระยะทางเฉลี่ยจากโลกไปดวงจันทร์คำนวณโดยองค์การ NASA 385,000 Km ก็ถือว่าปฏิบัติการครั้งนี้เข้าเป้าอย่างมาก   

 

 

อย่างไรก็ตามมุมมองภาพการเคลื่อนตัวของดวงจันทร์เข้าสู่เงามืดของโลกระหว่างประเทศไทยกับออสเตเรีย "กลับหัวกลับหางกัน" เพราะประเทศทั้งสองตั้งอยู่คนละซีกโลก ประเทศไทยอยู่ซีกโลกด้านเหนือ (northern hemisphere) ส่วนออสเตเรียอยู่ซีกโลกด้านใต้ (southern hemisphere) มุมมองทางดาราศาสตร์จึงกลับทางกัน 

 

 

 

การเคลื่อนตัวของราหูที่มองเห็นจากออสเตเรีย

 

 

การเคลื่อนตัวของราหูที่มองเห็นจากประเทศไทย

 

 Mr.Ken White เพื่อนผมที่ออสเตเรีย พี่แกเล่นนั่งกินไวน์แดงยี่ห้อ Dumont อย่างสบายใจปล่อยให้ Mr.Reg Travers ยืนขาแข็งถ่ายรูปราหูอมจันทร์อยู่ตามลำพัง อย่างว่าแหละครับแกรู้ดีว่าผมก็ชอบกินไวน์ก็เลยส่งภาพมาเยาะเย้ย........ เอ้าไม่ว่ากันครับถ้าผลงานมันเข้าเป้า  

 

 

สรุป

          การคำนวณระยะทางจากโลกไปดวงจันทร์ด้วยวิธีใหม่นี้ผมพัฒนาต่อยอดมาจากวิธีเดิมของท่าน Aristarchus of Samos นักคณิตศาสตร์ชาวกรีกเมื่อสองพันกว่าปีที่แล้ว โดยดำเนินการ ดังนี้

          1.ใช้กล้องดิจิต้อลถ่ายภาพดวงจันทร์ขณะที่กำลังเข้าสู่เงามืดของโลก (umbra) หรือกำลังออกจากเงามืดของโลกและนำมา download ลงใน Powerpoint

          2.สร้าง "ภาพเชิงซ้อน" รูปวงกลมให้มีรูปร่างและขนาดเท่ากับเงามืดของโลก และสร้างวงกลมอีกอันหนึ่งให้มีรูปร่างเท่ากับขนาดของดวงจันทร์

          3.วัดขนาดความยาวของเส้นผ่าศูนย์กลาง "เงามืดของโลก" และ "ดวงจันทร์" เป็นหน่วย ซม. หรือหน่วยอะไรก็ได้ และนำตัวเลขทั้งสองไปเข้าสมการ

 

 

 

          4.สูตรการคำนวณใหม่นี้ใช้ได้ทั้งปรากฏการณ์จันทรุปราคาเต็มดวง และจันทรุปราคาบางส่วน เพราะใช้ภาพถ่ายดวงจันทร์แหว่ง (เนื่องจากเงามืดของโลก) เพียง 1 ภาพ ต่างกับวิธีการดั้งเดิมของกรีกโบราณที่ต้องใช้ "ปรากฏการณ์จันทรุปราคาเต็มดวงเท่านั้น